
Letzter Schultag: 28.07. : ein höchst interessantes Datum! Ebenso 22.07. als 28-6 = 22:
In der griechischen Mathematik finden wir im IX.Buch der "Elemente" des Euklid eine weitere Deutung der Zahl "28". Sie gehört dort zu den so genannten vollkommenen Zahlen. (Von ihm stammt übrigens auch die obige Formel im 1.Bild.)
Eine Zahl heisst nach Euklid vollkommen, wenn sie gleich der Summe ihrer echten Teiler ist.
Die kleinste vollkommene Zahl ist die "6", denn ihre echten Teiler sind 1, 2, und 3, und deren Summe 1+2+3=6 ist wieder die Zahl selbst. Die zweitgrösste ist "28" mit den Teilern 1, 2, 4, 7, 14 und 1+2+4+7+14=28. Notabene: Sie ist auch die Zahl des Mondes bzw. des Monatszyklus der Frau. Unterhalb von 10.000 gibt es nur noch zwei weitere: "496" und "8128".

Die einzelnen Szenen sind so komponiert, dass die jeweils wichtigste Situation auf der linken Seite des zugehörigen Sektors dargestellt wird. Das Tischgemälde war dazu bestimmt, entgegen dem Uhrzeigersinn umschritten zu werden. Übrigens kommen insgesamt genau 28 Personen in den 7 Teilsektoren vor.
In Zentrum des Bildes thront Christus, von ihm gehen genau 128 Strahlen aus, die auch den Teufel treffen: 128 = 100 + 28 : "100" als biblische Zahl, die "28" als Art Überschuss für die Heimholung des Teufels.
Außen in den 4 Medaillons finden sich Szenen zu den 4 letzten Dingen des Lebens (Tod, Himmelfahrt, Geburt,..)
Kehren wir nun zu den vollkommenen Zahlen zurück:

Im Laufe der Jahre hat sich aus den vollkommenen Zahlen-Blumen ein Seitentrieb entwickelt, der im letzten Bild blau dargestellt ist und der uns direkt zu weiteren Pflanzen meines Gartens, den so genannten Mersenne-Zahlen, weiterführt.
Stellen Sie sich vor, Sie müssten herausfinden,ob
1234567890280987654321
eine Primzahl ist oder nicht. (Primzahlen sind bekanntlich jene Zahlen, die genau zwei Teiler besitzen.) Natürlich könnten Sie auch ohne diese Erkenntnis leben, aber für einen echten Mathematiker sind Primzahlen eine Herausforderung, zumal es heute durchaus sehr konkrete, wichtige Anwendungen vor allem in der Kryptographie gibt.
Der Amerikaner Frank Cole benötigte 1903 die "Sonntage dreier Jahre", um in seiner Freizeit zu zeigen, dass Mersenne´s Vermutung nicht stimmt. Er konnte zeigen, dass gilt:


An möglichst großen Primzahlen (nicht nur vom Mersenne-Typ) ist man heute aus zweierlei Gründen so interessiert: zum einen dienen sie als Testobjekte für die Rechenleistung eines Computers, zum andern sind sie Basis einer modernen Verschlüsselung im Rahmen der Public-Key-Verfahren.
Es ist beispielsweise sehr einfach, zwei Primzahlen p und q miteinander zu multiplizieren, aber fast unmöglich (und das ist die Falltür), aus dem Produkt wieder auf die ursprünglichen Primfaktoren zu schließen: vorausgesetzt, p und q sind groß genug.Die Idee zu dieser Falltürfunktion hatten 3 Herren vom MIT: Rivest, Shamir und Adleman, weshalb das zugehörigen Verfahren heute allgemein als RSA-Verfahren bekannt ist.
Man hatte damals noch kein sicheres Wissen, wie groß denn eine solche Primzahl zu sein habe. Im Jahre 1977 druckte die Zeitschrift "Scientific American" eine 129 Stellen lange natürliche Zahl ab, welche als Produkt aus zwei der Öffentlichkeit unbekannten Primzahlen entstanden war. Als Preis wurden $100 ausgesetzt für denjenigen, der es schafft, die beiden Primfaktoren zu berechnen. Der geringe Lohn basierte auf der Annahme, dass innerhalb kürzester Zeit eine diesbezügliche Lösung gefunden würde.

Aber nichts geschah! Über 16 Jahre blieb das Problem trotz intensiver Bemühungen ungelöst.

Damit hatte der RSA-Algorithmus seine erste Feuerprobe mit Bravour bestanden. Er war zwar nicht 100%-ig sicher, doch lässt sich seine momentane Sicherheit leicht dadurch erhöhen, dass man noch größere Primzahlen verwendet: z.B. eine RSA-Zahl mit 308 Stellen. Dafür wäre beim heutigen Stand der Technik eine astronomische Rechenleistung von nahezu einer halben Milliarde Jahre notwendig, vorausgesetzt, niemand findet einen schnellen Algorithmus zur Primfaktorzerlegung großer Zahlen, was nicht ganz ausgeschlossen werden kann. Momentan sind sich die Mathematiker einig, das die erforderliche Primfaktorzerlegung ein so genanntes NP-Problem (wie auch das Problem des Handlungsreisenden ein solches ist) darstellt, d.h. seine Lösung ist nur in nicht-polynomialer Zeit möglich.
Zum Schluss folgt noch eine kleine Anwendung des RSA-Verfahrens im Bankenbereich: konkret der Abhebevorgang von Geld mittels PIN an einem Geld- Automat.
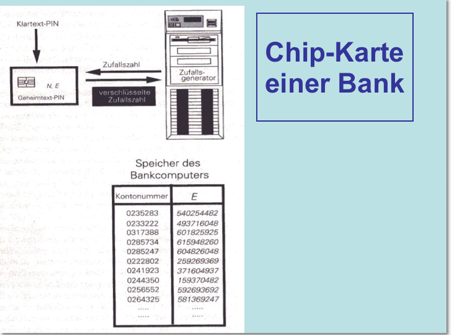
Am Bankautomat (oder einer elektronischen Händlerkasse) wird nun die Eingabe der PIN-Nummer verlangt, diese innerhalb der Chipkarte mit dem vorhandenen Kartenschlüssel chiffriert und mit der gespeicherten, verschlüsselten Geheim-PIN verglichen. Anschließend folgt eine weitere Kartenkontrolle: der Bankrechner (oder Kassenrechner) generiert eine einmalige Zufallszahl, berechnet daraus selbst mithilfe des Authentifikations-Algorithmus die zugehörige verschlüsselte Zufallszahl, lässt die analoge Rechnung innerhalb der Chipkarte ablaufen und vergleicht wieder die beiden Ergebnisse. Erst wenn jetzt völlige Übereinstimmung auftritt, kann der eigentliche Buchungsvorgang abgewickelt werden.
Damit endet der Rundgang durch meinen mathematischen Garten...